Problem Description
The Rascal Triangle definition is similar to that of the Pascal Triangle. The rows are numbered from the top starting with 0. Each row n contains n+1 numbers indexed from 0 to n. Using R(n,m) to indicte the index m item in
the index n row:
R(n,m) = 0 for n < 0 OR m < 0 OR m > n
The first and last numbers in each row(which are the same in the top row) are 1:
R(n,0) = R(n,n) = 1
The interior values are determined by (UpLeftEntry*UpRightEntry+1)/UpEntry(see the parallelogram in the array below):
R(n+1, m+1) = (R(n,m) * R(n,m+1) + 1)/R(n-1,m)
Image may be NSFW.
Clik here to view.
Write a program which computes R(n,m) theImage may be NSFW.
Clik here to view. element of theImage may be NSFW.
element of theImage may be NSFW.
Clik here to view. row
of the Rascal Triangle.
row
of the Rascal Triangle.
The first and last numbers in each row(which are the same in the top row) are 1:
The interior values are determined by (UpLeftEntry*UpRightEntry+1)/UpEntry(see the parallelogram in the array below):
Clik here to view.

Write a program which computes R(n,m) theImage may be NSFW.
Clik here to view.
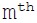 element of theImage may be NSFW.
element of theImage may be NSFW.Clik here to view.
 row
of the Rascal Triangle.
row
of the Rascal Triangle.Input
The first line of input contains a single integer P, (1 <= P <= 1000), which is the number of data sets that follow. Each data set is a single line of input consisting of 3 space separated decimal integers. The first integer
is data set number, N. The second integer is row number n, and the third integer is the index m within the row of the entry for which you are to find R(n,m) the Rascal Triangle entry (0 <= m <= n <= 50,000).
Output
For each data set there is onr line of output. It contains the data set number, N, followed by a single space which is then followed by thr Rascal Triangle entry R(n,m) accurate to the integer value.
Sample Input
5 1 4 0 2 4 2 3 45678 12345 4 12345 9876 5 34567 11398
Sample Output
1 1 2 5 3 411495886 4 24383845 5 264080263
/*
一道规律题,通过找规律不难发现要求的数便是
(x-y)*y+1
我就不多说了,规律推出来就相当简单了
*/
#include <stdio.h>
int main()
{
int t,n;
__int64 x,y;
scanf("%d",&t);
while(t--)
{
scanf("%d%I64d%I64d",&n,&x,&y);
if(x == 0 || x == y || y == 0)
{
printf("%d 1\n",n);
continue;
}
printf("%d %I64d\n",n,(x-y)*y+1);
}
return 0;
}
作者:libin56842 发表于2013-5-5 20:48:29 原文链接
阅读:27 评论:0 查看评论